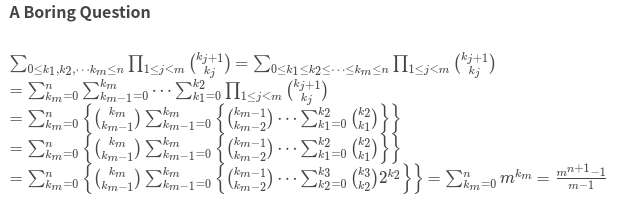2016 Hdu 多校赛第六场

发表于   |   分类于

Hdu 5793 A Boring Question

链接

A Boring Question

题意

$\sum_{0\leq k_{1},k_{2},\cdots k_{m} \leq n} \prod_{1\leqslant j <m}\binom{k_{j+1}}{k_{j}} \% 1000000007=?$
其中$\binom{k_{j+1}}{k_{j}}=\frac{k_{j+1}!}{k_{j}!\left ( k_{j+1}-k_{j} \right )!}$

分析

打表找规律得出的，官方题解推导：
Hdu5793

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include<stdio.h>
#include<string.h>
typedef long long LL;
const int mod=(int)1e9+7;
LL powMod(LL a,LL b)
{
    LL ans=1;
    while(b){
        if(b&1)
            ans=ans*a%mod;
        b>>=1;
        a=a*a%mod;
    }
    return ans;
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--){
        LL n,m;
        scanf("%lld%lld",&n,&m);
        LL ans=(powMod(m,n+1)-1+mod)%mod*powMod(m-1,mod-2)%mod;
        printf("%lld\n",ans);
    }
    return 0;
}

Hdu 5794 A Simple Chess

链接

A Simple Chess

题意

有一个n*m的棋盘，有一个棋子要从(1,1),走到(n,m),问有多少中走法？
每次只能从往右下走日字形，且棋盘上有些障碍点，障碍点不能放棋子。

分析

若不考虑障碍，从(a,b)点到(c,d)点，设走(2,1)有lt步，(1,2)有up步,则
lt=(2*(c-a)-(d-b))/3,up=(2*(d-b)-(c-a))/3;
可以计算出(1,1)到(n,m)以及各个障碍物的方案数，依次从上往下，从左往右
计算各个障碍对其他点的方案的贡献值并更新其他点，最终可算出到(n,m)的方案数。
题中涉及到求组合数取余，数据范围较大，需用到Lucas定理:
Lucas

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
const int N=105;
typedef long long LL;
const int MOD=110119;
struct Obs{
    LL x,y;
    LL rk;
    LL step;
}obs[N];
LL edge[N][N],fac[MOD+5];
void init()
{
    fac[0]=1;
    for(int i=1;i<=MOD;i++){
        fac[i]=fac[i-1]*i%MOD;
    }
}
bool calStep(LL a,LL b,LL c,LL d,LL& up,LL& lt)
{
    lt=2*(c-a)-(d-b);
    up=2*(d-b)-(c-a);
    if(lt<0||lt%3||up<0||up%3)
        return false;
    lt/=3;
    up/=3;
    return true;
}
LL powMod(LL a,LL b)
{
    LL ans=1;
    a%=MOD;
    while(b){
        if(b&1)
            ans=ans*a%MOD;
        a=a*a%MOD;
        b>>=1;
    }
    return ans;
}
LL comb(LL n,LL m)
{
    if(m>n||m<0)
        return 0;
    if(m==0)
        return 1;
    return fac[n]*powMod(fac[n-m]*fac[m]%MOD,MOD-2)%MOD;
}
LL Lucas(LL n,LL m)
{
    if(m==0)
        return 1;
    return comb(n%MOD,m%MOD)*Lucas(n/MOD,m/MOD)%MOD;
}
void addObs(LL x,LL y,LL up,LL lt,int id)
{
    obs[id].x=x;
    obs[id].y=y;
    obs[id].rk=lt+up;
    obs[id].step=Lucas(up+lt,up);
}
void buildEdge(int k)
{
    memset(edge,-1,sizeof(edge));
    for(int i=0;i<k;i++){
        for(int j=i+1;j<k;j++){
            LL up,lt;
            if(calStep(obs[i].x,obs[i].y,obs[j].x,obs[j].y,up,lt)){
                edge[i][j]=Lucas(up+lt,up);
            }
        }
    }
}
bool cmp(Obs a,Obs b)
{
    if(a.rk!=b.rk)
        return a.rk<b.rk;
    return a.x<b.x;
}
int main()
{
    LL n,m,up,lt;
    int r,cas=1;
    init();
    while(scanf("%lld%lld%d",&n,&m,&r)!=EOF){
        printf("Case #%d: ",cas++);
        int k=0;
        bool flag=false;
        for(int i=0;i<r;i++){
            LL x,y;
            scanf("%lld%lld",&x,&y);
            if(x==n&&y==m)
                flag=true;
            if(!flag&&calStep(1,1,x,y,up,lt)){
                addObs(x,y,up,lt,k);
                k++;
            }
        }
        if(!calStep(1,1,n,m,up,lt)||flag){
            printf("0\n");
            continue;
        }
        addObs(n,m,up,lt,k);
        k++;
        sort(obs,obs+k,cmp);
        buildEdge(k);
        for(int i=0;i<k;i++){
            for(int j=i+1;j<k;j++){
                if(obs[i].x==obs[j].x&&obs[i].y==obs[j].y)
                    continue;
                if(edge[i][j]!=-1){
                    obs[j].step=(obs[j].step-obs[i].step*edge[i][j]%MOD)%MOD;
                    if(obs[j].step<0)
                        obs[j].step+=MOD;
                }
            }
        }
        printf("%lld\n",obs[k-1].step);
    }
    return 0;
}

Hdu 5795 A Simple Nim

链接

A Simple Nim

题意

普通的Nim博弈的基础上多了一个操作，可选择任意一堆物品，
将其分成三堆(不能分出空对)，求谁会赢得游戏

分析

sg[0]=0
当x=8k+7时sg[x]=8k+8，
当x=8k+8时sg[x]=8k+7,
其余时候sg[x]=x；（k>=0）
打表找规律可得，数学归纳法可证。

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include<stdio.h>
int main()
{
    int T;
    scanf("%d",&T);
    while(T--){
        int n;
        scanf("%d",&n);
        int ans=0;
        for(int i=1;i<=n;i++){
            int x;
            scanf("%d",&x);
            if(x%8==7)
                ans^=(x+1);
            else if(x&&x%8==0)
                ans^=x-1;
            else
                ans^=x;
        }
        if(ans==0)
            printf("Second player wins.\n");
        else
            printf("First player wins.\n");
    }
    return 0;
}

Hdu 5800 To My Girlfriend

链接

To My Girlfriend

题意

给定包含n个元素的集合，问存在多少个子集，满足：
其中有两个元素必选，两个元素必不选，其和为m（1<=m<=s)

分析

令dp[i][j][s1][s2]表示前i个物品填了j的体积，有s1个物品选为为必选，s2个物品选为必不选的方案数(0<=s1,s2<=2)，对于每一个物品，有四种状态：不选，选，必选，必不选，则有转移方程
dp[i][j][s1][s2] = dp[i - 1][j][s1][s2] +
dp[i - 1][j-a[i]][s1][s2] +
dp[i - 1][j - a[i]][s1 - 1][s2] +
dp[i - 1][j][s1][s2 - 1]，
边界条件为dp[0][0][0][0] = 1

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include<stdio.h>
#include<string.h>
typedef long long LL;
const int N=1005;
const int MOD=(int)1e9+7;
LL dp[2][N][3][3];
int n,s,a[N];
LL solve()
{
    memset(dp,0,sizeof(dp));
    dp[0][0][0][0]=1;
    bool now=0;
    for(int i=1;i<=n;i++){
        now=!now;
        for(int j=0;j<=s;j++){
            for(int s1=0;s1<3;s1++){
                for(int s2=0;s2<3;s2++){
                    bool last=!now;
                    dp[now][j][s1][s2]=dp[last][j][s1][s2];
                    if(j>=a[i])
                        dp[now][j][s1][s2]+=dp[last][j-a[i]][s1][s2];
                    if(j>=a[i]&&s1>0)
                        dp[now][j][s1][s2]+=dp[last][j-a[i]][s1-1][s2];
                    if(s2>0)
                        dp[now][j][s1][s2]+=dp[last][j][s1][s2-1];
                    dp[now][j][s1][s2]%=MOD;
                }
            }
        }
    }
    LL ans=0;
    for(int i=1;i<=s;i++){
        ans=ans+dp[now][i][2][2];
        ans=ans>MOD?ans-MOD:ans;
    }
    ans=ans*4%MOD;
    return ans;
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--){
        scanf("%d%d",&n,&s);
        for(int i=1;i<=n;i++)
            scanf("%d",&a[i]);
        printf("%lld\n",solve());
    }
    return 0;
}

Hdu 5802 Windows 10

链接

Windows 10

题意

某人需调节电脑音量，他有三种操作，按上键，按下键，休息，每次操作需一秒。
按上键：每次音量增加1，休息：音量不变
下键：第一次按音量减小1，若上一秒按下键音量降低了x,则这秒降低2x,
若上一秒按的上键，或休息，则这秒按下键减小1
求将音量p调到q至少要多少秒？

分析

贪心+dfs
比较直观的看法是使劲往下降，然后升回来
或者使劲往下降然后停顿然后再使劲往下降。。。
于是就能将问题变成一个子问题，然后dfs就好
需要注意的是由于按up键也可以打断连续向下的功效
所以应该记录停顿了几次，以后向上的时候用停顿补回来

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include<stdio.h>
#include<algorithm>
#define INF 0x3f3f3f
typedef long long LL;
using namespace std;
LL ans;
LL len,two[35];
void init()
{
    len=31;
    two[0]=0;
    LL tmp=1;
    for(int i=1;i<len;i++){
        tmp<<=1;
        two[i]=tmp-1;
    }
}
void dfs(LL now,LL ed,LL step,LL stop)
{
    int pos=lower_bound(two,two+len,now-ed)-two;
    LL tmp=now-two[pos];
    if(tmp==ed){
        ans=min(ans,step+pos);
    }
    else{
        LL up=ed-max(0LL,tmp);
        ans=min(ans,step+pos+max(0LL,up-stop));
        dfs(now-two[pos-1],ed,step+pos-1+1,stop+1);
    }
}
int main()
{
    int T;
    init();
    scanf("%d",&T);
    while(T--){
        LL p,q;
        scanf("%lld%lld",&p,&q);
        if(p<q){
            printf("%lld\n",q-p);
            continue;
        }
        ans=INF;
        dfs(p,q,0,0);
        printf("%lld\n",ans);
    }
    return 0;
}