2016 Hdu 多校赛第三场

发表于   |   分类于

Hdu 5752 Sqrt Bo

链接

Sqrt Bo

题意

$f(n)=\lfloor \sqrt{n}\rfloor,f^1(n)=f(n),f^y(n)=f(f^{y-1}(n))$
每计算一次函数f需一个单位时间，给定一个数n，问需要几个单位时间使得$f^y(n)=1$.若需超过5个单位时间输出”TAT”.

分析

由于有5次的这个限制，所以尝试寻找分界点。很容易发现是$2^{32}$，所以我们先比较输入的数字是否比这个大，然后再暴力开根复杂度是$O(\log\log n)$.注意n=0答案为0。

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<stdio.h>
#include<string.h>
#include<math.h>
int main()
{
    char str[150];
    while(scanf("%s",str)!=EOF){
        int n=strlen(str);
        if(n>15||(str[0]=='0'&&n==1)){
            printf("TAT\n");
            continue;
        }
        long long num=0;
        for(int i=0;i<n;i++){
            num=num*10+str[i]-'0';
        }
        int ans=0;
        while(num!=1){
            num=floor(sqrt(num*1.0));
            ans++;
        }
        if(ans>5)
            printf("TAT\n");
        else
            printf("%d\n",ans);
    }
    return 0;
}

Hdu 5753 Permutation Bo

链接

Permutation Bo

题意

$h_1\sim h_n$是$1\sim n$的排列，$h_0=h_{n+1}=0,f(h)=\sum_{i=1}^{n}{c_i[h_i>h_{i-1} and h_i>h_{i+1}]}$
已知 $c_1\sim c_n$,求 f(h)的期望

分析

根据期望的线性性，我们可以分开考虑每个位置对答案的贡献。
1)i在两端，对答案贡献为 ci/3
2)i不在两边，对答案贡献为ci/2

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<stdio.h>
#include<string.h>
int c[1010];
int main()
{
    int n;
    while(scanf("%d",&n)!=EOF){
        double sum=0;
        for(int i=1;i<=n;i++){
            scanf("%d",&c[i]);
        }
        if(n==1){
            printf("%d\n",c[1]);
            continue;
        }
        for(int i=1;i<=n;i++){
            if(i==1||i==n)
                sum+=c[i]/2.0;
            else
                sum+=c[i]/3.0;
        }
        printf("%lf\n",sum);
    }
    return 0;
}

Hdu 5754 Life Winner Bo

链接

Life Winner Bo

题意

一个国际象棋棋盘，有四种棋子，要从(1,1)走到(n,m)，两人轮流下棋，每次只能往右下方向走，先走到(n,m)的人赢，先手赢输出B，后手赢输出G，平局输出D。

分析

四种棋子的规则如下：
1、王（King）：横、竖、斜都可以走，每次限走一格，
若(n-1)和(m-1)都为偶数，先手必败，也可用SG函数处理
2、车（Rook）：横、竖均可走，不能斜走，格数不受限制，可以看成有两堆石子的尼姆博弈
3、马（Knight）：马走日，可用SG函数处理
4、后（Queen）：横、竖、斜都可以走，格数不受限制，可看成威佐夫博弈

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
#include<stdio.h>
#include<string.h>
#include<math.h>
#define N 1005
int n,m,sg_king[N][N],sg_knight[N][N];
void king()
{
    memset(sg_king,-1,sizeof(sg_king));
    sg_king[1][1]=0;
    for(int i=1;i<N;i++){
        for(int j=1;j<N;j++){
            if(sg_king[i-1][j]&&sg_king[i][j-1]&&sg_king[i-1][j-1])
                sg_king[i][j]=0;
            else
                sg_king[i][j]=1;
        }
    }
}
void knight()
{
    memset(sg_knight,-1,sizeof(sg_knight));
    sg_knight[1][1]=0;
    for(int i=1;i<=1000;i++){
        for(int j=1;j<=1000;j++){
            int x=-1,y=-1;
            if(i-2>=1&&j-1>=1)
                x=sg_knight[i-2][j-1];
            if(i-1>=1&&j-2>=1)
                y=sg_knight[i-1][j-2];
            if(x==0||y==0)
                sg_knight[i][j]=1;
            else if(x==1&&y==1)
                sg_knight[i][j]=0;
        }
    }
}
int main()
{
    int T;
    king();
    knight();
    scanf("%d",&T);
    while(T--){
        int type;
        scanf("%d%d%d",&type,&n,&m);
        if(type==1){  //king
            if(sg_king[n][m])
                printf("B\n");
            else
                printf("G\n");
        }
        else if(type==2){  //rook
            int res=(n-1)^(m-1);
            if(res)
                printf("B\n");
            else
                printf("G\n");
        }
        else if(type==3){  //knight
            if(sg_knight[n][m]==-1)
                printf("D\n");
            else if(sg_knight[n][m]==0)
                printf("G\n");
            else
                printf("B\n");
        }
        else if(type==4){
            int a=n-1,b=m-1;
            if(a>b){
                a=a^b;
                b=a^b;
                a=a^b;
            }
            int res=floor((b-a)*(1+sqrt(5.0))/2.0);
            if(res==a)
                printf("G\n");
            else
                printf("B\n");
        }
    }
    return 0;
}

Hdu 5755 Gambler Bo

链接

Gambler Bo

题意

给定一个只含{0,1,2}的n*m的矩阵。有一种操作：将(x,y)位置+2，
同时(x-1,y),(x+1,y),(x,y-1),(x,y+1)都会+1,若格子的值超过3，则需模3。
要求进行不超过2*n*m次操作将矩阵变为全0，数据保证至少有一组解。

分析

问题可以转化为一个模3域下的方程，对每个位置可以列出一个方程，
即覆盖到这个位置的操作造成的影响和要使得这个位置变为0。
对于同一格，操作三次后又会回到为操作前的状态，即每个格最多操作两次，总次数不超过2*n*m
列出同余方程组后，进行高斯消元，涉及到除法的地方需要求逆元。

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
#define mod 3
const int N=1000;
int a[N][N],ans[N],sum;
const int dx[4]={0,0,1,-1};
const int dy[4]={1,-1,0,0};
int gcd(int a,int b)
{
    return b==0?a:gcd(b,a%b);
}
int Lcm(int a,int b)
{
    return a/gcd(a,b)*b;
}
int gauss(int n,int m)
{
    int row=0,col=0;
    for(;row<n;row++,col++){
        int notZero=row;
        //求第一个第col列非零的行
        for(int i=row;i<n;i++)
            if(a[i][col]){
                notZero=i;
                break;
            }
        if(notZero==n){ //若col列都为0
            row--;
            continue;
        }
        if(notZero!=row){ //找到非零行与当前行交换
            for(int j=0;j<=m;j++)
                swap(a[row][j],a[notZero][j]);
        }
        //本题一定有解，不必判断方程是否无解
        for(int i=row+1;i<n;i++){
            if(a[i][col]){
                int lcm=Lcm(a[row][col],a[i][col]);
                int t1=lcm/a[row][col];
                int t2=lcm/a[i][col];
                for(int j=col;j<=m;j++)
                    a[i][j]=((a[i][j]*t1-a[row][j]*t2)%mod+mod)%mod;
            }
        }
    }
    memset(ans,0,sizeof(ans));
    sum=0;  //操作的总次数
    for(int i=n-1;i>=0;i--){
        if(a[i][i]==0)
            continue;
        int temp=a[i][m];
        for(int j=i+1;j<m;j++){
            temp=((temp-a[i][j]*ans[j])%mod+mod)%mod;
        }
        //ans[i]=temp/a[i][i] 需求逆元
        //ans[i]=temp*(a[i][i]^mod-2)=temp*a[i][i]
        ans[i]=temp*a[i][i]%mod;
        sum+=ans[i];
    }
    return 0;
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--){
        int n,m;
        scanf("%d%d",&n,&m);
        memset(a,0,sizeof(a));
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                int x;
                scanf("%d",&x);
                a[i*m+j][i*m+j]=2;
                a[i*m+j][n*m]=(-x+mod)%mod;
                for(int k=0;k<4;k++){
                    int r=i+dx[k];
                    int c=j+dy[k];
                    if(r>=0&&r<n&&c>=0&&c<m)
                        a[i*m+j][r*m+c]=1;
                }
            }
        }
        gauss(n*m,n*m);
        printf("%d\n",sum);
        for(int i=0;i<n*m;i++){
            int r=i/m+1;
            int c=i%m+1;
            for(int j=0;j<ans[i];j++)
                printf("%d %d\n",r,c);
        }
    }
    return 0;
}

Hdu 5761 Rower Bo

链接

Rower Bo

题意

有一条沿水平方向的河，Bo在(0,a)点，他想到源点(0,0),已知静水中速度v1，水流速v2,
v1的方向一直朝向原点，求需要多就到达，若到不了输出”Infinity”

分析

官方题解推导如下：
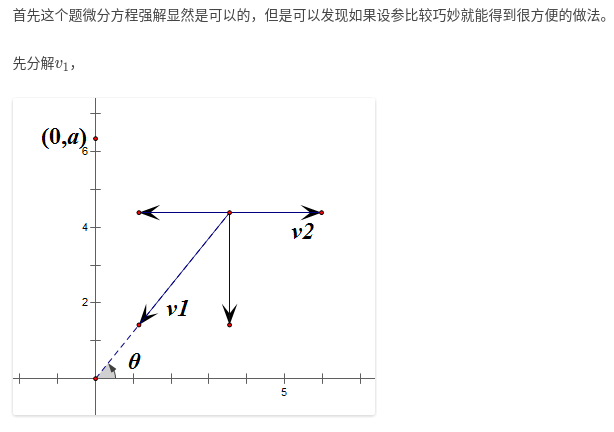
hdu5761
hdu5761

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include<stdio.h>
int main()
{
    int a,v1,v2;
    while(scanf("%d%d%d",&a,&v1,&v2)!=EOF){
        if(a==0)
            printf("0\n");
        else if(v1<=v2)
            printf("Infinity\n");
        else{
            double ans=(double)a*v1/(v1*v1-v2*v2);
            printf("%lf\n",ans);
        }
    }
    return 0;
}

Hdu 5762 Teacher Bo

链接

Teacher Bo

题意

已知n个点，求是否存在(A,B,C,D)满足A和B的曼哈顿距离跟C和D的曼哈顿距离相等.
其中A与B点不能为统一点，C与D不能为统一点，B和C可为同一点
A(x1,y1),B(x2,y2),AB的曼哈顿距离=|x1-x2|+|y1-y2|

分析

考虑一种暴力,每次枚举两两点对之间的曼哈顿距离,并记录每种距离是否出现过,
如果某次枚举出现了以前出现的距离就输 YES,否则就输 NO.
注意到曼哈顿距离只有 O(M)种,根据鸽笼原理,上面的算法在 O(M)步之内一定会停止.
一组数据的时间复杂度 $O(\min{N^2,M})$

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
const int N=100010;
struct point{
    int x,y;
}p[N];
bool vis[N<<1];
int main()
{
    int T;
    scanf("%d",&T);
    while(T--){
        int n,m;
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n;i++){
            scanf("%d%d",&p[i].x,&p[i].y);
        }
        memset(vis,false,sizeof(vis));
        bool flag=false;
        for(int i=1;i<=n&&!flag;i++){
            for(int j=i+1;j<=n;j++){
                int d=abs(p[i].x-p[j].x)+abs(p[i].y-p[j].y);
                if(!vis[d])
                    vis[d]=true;
                else{
                    flag=true;
                    break;
                }
            }
        }
        if(flag)
            printf("YES\n");
        else
            printf("NO\n");
    }
    return 0;
}