Hdu 5396 Expression
链接
Expression
题意
给定n个数和n-1个操作符(+,-,*),求所有不同的运算顺序的结果的和
注:这里乘法和加减没有优先级之分。如1+2*3可能是1+(2*3)或(1+2)*3
分析
区间DP
若一个表达式有num个操作符,则有num!种不同的计算方式
用dp[l][r]表示第l个数到第r个数组成的所有可能性的表达式和,枚举最后操作k,
若为加号,对于右边不同的组合(r-k-1)!种,左边的数每次都要被加一次,
同理左边不同的组合(k-l)!种,右边的数每次也要被加一次。
即$ temp=(r-k-1)!*dp[l][k]+(k-l)!*dp[k+1][r] $,
减法同理$ temp=(r-k-1)!*dp[l][k]-(k-l)!*dp[k+1][r] $
若为乘法$ temp=dp[l][k]*dp[k+1][r] $,乘法满足分配律,算出分别左右情况的总和相乘即可
还有一点,左边的顺序和右边的顺序的确定,假设左边有f1个符号,右边有f2个符号,
就有$cnt=\binom{f1+f2}{f1}$种组合,即左边和右边的操作顺序不同,运算顺序也不同
即$ dp[l][r]+=temp*cnt $
参考代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| #include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
typedef long long LL;
const LL MOD=1000000007LL;
const int N=105;
LL dp[N][N],c[N][N],f[N];
char ope[N];
void init()
{
c[0][0]=f[0]=1;
for(int i=1;i<N;i++){
c[i][0]=c[i][i]=1;
f[i]=f[i-1]*i%MOD;
for(int j=1;j<N;j++)
c[i][j]=(c[i-1][j-1]+c[i-1][j])%MOD;
}
}
void solve(int n)
{
for(int len=2;len<=n;len++){
for(int l=0;l+len<=n;l++){
int r=l+len-1;
LL temp;
for(int k=l;k<r;k++){
if(ope[k]=='+')
temp=(f[r-k-1]*dp[l][k]%MOD+f[k-l]*dp[k+1][r]%MOD)%MOD;
else if(ope[k]=='-')
temp=((f[r-k-1]*dp[l][k]%MOD-f[k-l]*dp[k+1][r]%MOD)%MOD+MOD)%MOD;
else if(ope[k]=='*')
temp=dp[l][k]%MOD*dp[k+1][r]%MOD;
temp=temp*c[len-2][k-l]%MOD;
dp[l][r]=(dp[l][r]+temp)%MOD;
}
}
}
}
int main()
{
int n;
init();
while(scanf("%d",&n)!=EOF){
memset(dp,0,sizeof(dp));
for(int i=0;i<n;i++)
scanf("%I64d",&dp[i][i]);
scanf("%s",ope);
solve(n);
printf("%I64d\n",dp[0][n-1]);
}
return 0;
}
|
Hdu 5399 Too Simple
链接
Too Simple
题意
有m个函数,$f_1,f_2,\cdots,f_m:{1,2,\cdots,n}\to{1,2,\cdots,n}$
即$x \in {1,2,\cdots,n},f(x)\in {1,2,\cdots,n}$
给定n和m,即m个函数对应的函数值,若为-1,则该函数未知,求有多少种可能性满足
$$f_1(f_2(\cdots f_m(i)))=i (1\leq i\leq n)$$
分析
首先要求每个$f_i$是个排列,即当i≠j时,f[i]≠f[j] ,否则如果某个$f_i$
将两个数映射向同一个数,那么最后这两个数得到的值一定相同。
如果还剩一个位置为-1,那么这个排列是唯一确定的,只有一种
若有cnt个-1,则有$(n!)^{cnt-1}$种可能性
若所有的函数都确定,除了满足必须都是一个排列外,还得满足题设的条件
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
| #include<stdio.h>
#include<string.h>
typedef long long LL;
const int N=105;
const LL MOD=1000000007LL;
LL f[N];
int n,m,y[N][N];
void init()
{
f[0]=f[1]=1;
for(int i=2;i<N;i++)
f[i]=f[i-1]*i%MOD;
}
LL powMod(LL a,LL b)
{
LL ans=1;
while(b){
if(b&1)
ans=ans*a%MOD;
a=a*a%MOD;
b>>=1;
}
return ans;
}
bool judge()
{
for(int i=1;i<=n;i++){
int x=i;
for(int j=m;j>=1;j--)
x=y[j][x];
if(x!=i)
return false;
}
return true;
}
int main()
{
init();
while(scanf("%d%d",&n,&m)!=EOF){
int cnt=0;
bool flag=true;
for(int i=1;i<=m;i++){
scanf("%d",&y[i][1]);
if(y[i][1]==-1)
cnt++;
else{
bool vis[N]={false};
vis[y[i][1]]=true;
for(int j=2;j<=n;j++){
scanf("%d",&y[i][j]);
if(!vis[y[i][j]])
vis[y[i][j]]=true;
else
flag=false;
}
}
}
if(!flag)
printf("0\n");
else if(cnt==0){
if(judge())
printf("1\n");
else
printf("0\n");
}
else
printf("%I64d\n",powMod(f[n],cnt-1));
}
return 0;
}
|
Hdu 5400 Arithmetic Sequence
链接
Arithmetic Sequence
题意
给定n个数{a1,a2..an},及d1,d2,求有多少个区间[l,r]满足[l,i]为公差为d1的等差数列,
[i,r]为公差为d2的等差数列 $(i \in [l,r]) $
分析
对于单个数肯定满足条件,如某区间只形成公差为d1或d2的等差数列也满足题意
对于长度大于等于2的区间,可以枚举起点i,找到最长的满足d1,d2的序列j
那么就有 $\binom{j-i+1}{2}=(j-i+1)*(j-i)/2$个满足条件,然后i再从j开始枚举
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| #include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
const int N=100010;
typedef long long LL;
LL a[N],b[N];
int main()
{
int n,d1,d2;
while(scanf("%d%d%d",&n,&d1,&d2)!=EOF){
for(int i=1;i<=n;i++)
scanf("%I64d",&a[i]);
for(int i=1;i<n;i++)
b[i]=a[i+1]-a[i];
int i=1;
LL ans=n;
while(i<n){
int j=i;
while(j<n&&b[j]==d1) j++;
while(j<n&&b[j]==d2) j++;
LL len=j-i+1;
ans+=len*(len-1)/2;
if(len!=1) i=j;
else i++;
}
printf("%I64d\n",ans);
}
return 0;
}
|
Hdu 5402 Travelling Salesman Problem
链接
Travelling Salesman Problem
题意
给定n*m的迷宫,每个格的数都是非负的,Teacher Mai想要从迷宫的左上角(1,1)到
迷宫的右下角(n,m),每次只能走到相邻的格,其不能走出迷宫,每个格最多只能走一次
求走过的路径的整数之和最大为多少以及他走的路径。
分析

因为每个格子都是非负整数,而且规定每个格子只能走一次,所以为了使和尽可能大,必定是走的格子数越多越好。这样我们就需要考虑一下是不是所有的格子都可以走。
若n、m中至少有一个是奇数的话,必然能够遍历每一个格子,
m为奇数
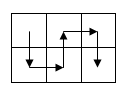
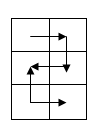
n为奇数时
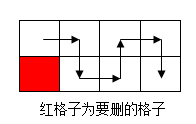
当n、m都为偶数,根据棋盘黑白染色可得,当假设(1,1)与(n,m)都为黑色,那么这条路径势必黑色格子数会比白色格子数多1,而棋盘中黑白格子数是相等的,所以棋盘中有一个白格子不会被经过。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
| #include<stdio.h>
const int INF=0x3f3f3f3f;
const int N=105;
int main()
{
int n,m;
while(scanf("%d%d",&n,&m)!=EOF){
int sum=0,x,minx=INF,posi,posj;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
scanf("%d",&x);
sum+=x;
if(((i+j)&1)&&x<minx){
minx=x;
posi=i;
posj=j;
}
}
if(m&1||n&1){
printf("%d\n",sum);
if(n&1){
for(int i=1;i<=n;i++){
for(int j=1;j<m;j++){
if(i&1) printf("R");
else printf("L");
}
if(i<n) printf("D");
else printf("\n");
}
}
else{
for(int j=1;j<=m;j++){
for(int i=1;i<n;i++){
if(j&1) printf("D");
else printf("U");
}
if(j<m) printf("R");
else printf("\n");
}
}
}
else{
printf("%d\n",sum-minx);
for(int i=1;i<=n;i+=2){
if(i==posi||i+1==posi){
for(int j=1;j<posj;j++){
if(j&1) printf("D");
else printf("U");
printf("R");
}
if(posj<m) printf("R");
for(int j=posj+1;j<=m;j++){
if(j&1) printf("U");
else printf("D");
if(j<m) printf("R");
}
if(i<n-1) printf("D");
}
else if(i<posi){
for(int j=1;j<m;j++)
printf("R");
printf("D");
for(int j=1;j<m;j++)
printf("L");
if(i<n-1)
printf("D");
}
else{
for(int j=1;j<m;j++)
printf("L");
printf("D");
for(int j=1;j<m;j++)
printf("R");
if(i<n-1)
printf("D");
}
}
printf("\n");
}
}
return 0;
}
|



