Hdu 5301 Buildings
链接
题意
有块地为n*m列的矩阵,要建造矩形公寓来完全覆盖这块地((x,y)方格除外)
且每个公寓必须有窗户,窗户只能设在这块地的矩阵的边缘上。
求满足条件的方案中公寓最大面积的最小值
分析
相当于用矩形填充nm的矩阵,且矩形至少有一条边在nm矩阵的边界上
若不考虑(x,y)方格被删除,ans=(min(m,n)+1)/2;
删除(x,y)后,若 m=n且n为奇数,且(x,y)在中心点,ans=ans-1;
否则 如图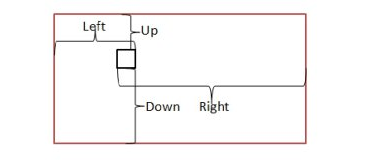
与(x,y)上下左右相邻点,只能往三个方向建公寓,对于这四个点
分别取对应的三个方向建公寓的最小面积s=min(s1,s2,s3);
ans=max(ans,s);
参考代码
1 | #include<stdio.h> |
Hdu 5303 Delicious Apples
链接
题意
一个环形道上有n个苹果树,第i棵树与仓库的顺时针距离为xi,树上有ai个苹果,仓库在位置0
你有一个容量为k的篮子,要从仓库出发去摘苹果,篮子装满后要回到起点清空篮子,
问你从起点出发,摘完所有苹果所走的最短路程。
分析
从起点可以顺时针或逆时针出发,最后的结果肯定是
顺时针取一定的苹果所走的最短路与逆时针走的最短路的和。
那么设dp[2][i],0代表顺时针,1代表逆时针,i代表取的苹果数,
值为取完i个苹果回到原点的最短路程。x[i]为第i个苹果所在的位置。
以顺时针为例,如果2*x[i] <L,那么后来走的路程为2*x[i],反之,为L;
转移方程:
dp[0][i] = min(dp[0][i],dp[0][i-j]+(2*x[i] <L ? 2*x[i] : L)) (1 <= j <= k)
因为dp[0][i]是非递减的,所以优化方程:
dp[0][i] = dp[0][i-k]+(2*x[i] <L ? 2*x[i] : L)
参考代码
1 | #include<stdio.h> |
Hdu 5305 Friends
题意
有n个人,m组关系,表示谁和谁是朋友关系
朋友分为线上朋友和线下朋友,
求满足每个人的线上朋友数和线下朋友数相同
有多少种的情况
分析
题中n<=8,m<=n(n-1)/2,对于每组朋友关系
要么为线上,要么为线下,dfs加剪枝
要保证每个人线上朋友和线下朋友人数相等,
则每个人的朋友数都为偶数,且总边数m为偶数,否则输出0
代码
1 | #include<stdio.h> |
Hdu 5308 I Wanna Become A 24-Point Master
链接
I Wanna Become A 24-Point Master
题意
$有n个数 a_1,a_2…a_n,它们的值都为n $
每次操作可以选两个未进行操作的数进行 “+”,”-“,”*”,”/“
第i次操作为a b c:其中a,c为数组下标,b为操作符, 则A[n+i]=A[a] b A[c];
要进行 n-1 次操作,使得最后数组2n-1的值为24
需要满足的条件:每个数都有且仅能用一次(包括新生成的数)
除法为小数除法,允许得到分数
若能找到满足条件的操作,输出这n-1次操作,否则输出-1
分析
24=4*6=3*8
可以构造 6个n相加,再用和除以n,得到6,4个n相加再除以n得到4
然后6*4=24, 这样 n最少为 12
同理构造 8*3,n最少为13
对于剩下未用的数,先让n-n=0,再由0乘上未用的数得到0,最后让0+24=24
所以对于 12+2k (k为自然数)构造 4*6
13+2k 构造 3*8
对于1-3,找不到符合条件的操作,输出-1
4-11,可以手算直接输出
注:n=5时 可以由 5*(5-(5/5)/5) 得到24 (允许小数除法)
参考代码
1 | #include<stdio.h> |