Hdu 4889 Scary Path Finding Algorithm
题意
给了一段程序,但这段程序有bug,给定一个C,求一组测试数据,使得程序会输出’doge’
分析
代码中只要所有点出队列的总次数大于C,就会输出 ‘doge’
但是C最大到 23333333,而顶点数n不超过100,
那么肯定要使出队列总次数达到指数级才行,即肯定有顶点会重复进入多次
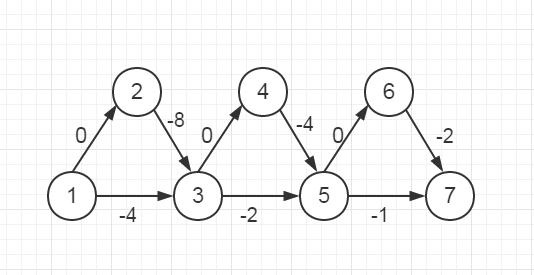
如上图所示,设p为奇数顶点,p+2可由 p或p+1到达,
由 p 可到达 p+1,p+2,要保证 p+2 多次进入队列,必须由p+1点开始松弛前出队列,
才能再次进入,将图中看成有多个包含p,p+1,p+2的小三角形,
则 $c_{i} < a_{i} $
这样松弛p点时,会把p+2放在队首,p+1放在队尾,p+2会先出队列
松弛p+1点时 要保证p+2再次进入队列 则 w(p->p+2)>w(p->p+1->p+2)
即 $ a_{i}+b_{i}<c_{i} $
p+2点要由 p点再次进入,则
$a_{i} + b_{i} + c_{i+1} < c_{i} + a_{i+1} + b_{i+1}$
即$ ( a_{i} + b_{i}- c_{i} ) + ( c_{i+1} - a_{i+1} -b_{i+1} )< 0 $
假设 第一个括号内 得 -2x ,第二个括号内得 x,则等式恒成立,
即可取 $ a_i =2a_{i+1}, b_i =2b_{i+1}, c_i =2c_{i+1} $
综合上诉三个不等式得 若共有N个三角形,
第i个三角形 $ a_i =0, b_i =-2^{N-i+1}, c_i = -2^{N-i} $
设 f(i)为顶点 i进队列的次数 则 f(i+2)=2f(i)
设 F(i)为第1点到 2i+1点所有点的总次数 则F(i)>$ 1+2^1+2^2+…+2^i=2^{i+1} $
即当三角形个数 N=24,$ F(i)> 2^{25} -1 > 23333333 $ 即可
此时 顶点个数 n=2N+1, 边数 m=3N
参考代码
1 | #include<stdio.h> |
Hdu 4891 The Great Pan
链接
题意
理解方法最少有一种,ans = 1
1.{}内的|个数为n,那么就是ans*=(n+1)
2.$$内的连续空格独立理解,每有一个连续的n个空格,ans*=(n+1)
3.输出理解方案数,超过100000输出doge
4.{},$$不会有嵌套,要注意运算时ans可能超出int型,要用long long
分析
模拟即可
代码
1 | #include<stdio.h> |
Hdu 4893 Wow! Such Sequence!
链接
题意
有n个数,初始都是0,可以进行3种操作
1 k d - 即第k个数加d
2 l r - 查询区间 [l,r]的和
3 l r - 将ai改为最接近于它的斐波那契数(l<=i<=r),即 |fib[j]-ai| 最小
先要进行m次操作,对于第2种操作,输出给定区间和
分析
对于操作1,单点更新,比较简单,lgn时间即可
但是操作3,区间更新,如果不加优化的直接将需要结点全部更新,时间效率很低
解法1
可以加一个flag,用来标记结点对应区间是否都为fib数
如果某区间是fib数,再进行3操作时,其值肯定不需要变,因为fib数肯定和它本身最接近
这样对于以该结点为根的子树都不需要更新,时间复杂度会大大降低
若需要更新的区间不是fib数,则更新
解法2
延迟标记法
若父结点更新为fib数,对其标记表示子孩子还未更新,等到需要用到子孩子时再更新,
并把标记转移到子孩子结点
但是更新结点时,若每次遍历fib数去找最接近的值很费时,
可以另设一个sumF结点存某结点所表示的区间为最接近的fib数的总和
代码1
1 | #include<stdio.h> |
代码2
1 | #include<stdio.h> |