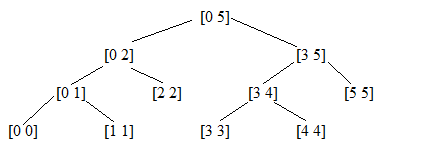
第一次接触线段树,发现理解基本思想后,线段树的基本运用还是很简单的
单点更新 HDU 1754 I Hate It 链接 I Hate It
题意 中文题,题意不用解释。。
分析 单点更新,求区间最值
参考代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 #include <stdio.h> #include <algorithm> const int N=200000 ;using namespace std ;int a[N+10 ],tree[2 *N+10 ],ans;void pushUp (int node) tree[node]=max(tree[node*2 ],tree[node*2 +1 ]); } void build (int l,int r,int node) if (l==r){ tree[node]=a[l]; return ; } int mid=(l+r)>>1 ; build(l,mid,node*2 ); build(mid+1 ,r,node*2 +1 ); pushUp(node); } void update (int l,int r,int node,int pos,int val) if (l==r){ tree[node]=val; return ; } int mid=(l+r)>>1 ; if (mid>=pos) update(l,mid,node*2 ,pos,val); else update(mid+1 ,r,node*2 +1 ,pos,val); pushUp(node); } void query (int l,int r,int node,int ql,int qr) if (ql<=l&&r<=qr){ ans=max(ans,tree[node]); return ; } int mid=(l+r)>>1 ; if (mid>=ql) query(l,mid,node*2 ,ql,qr); if (mid<qr) query(mid+1 ,r,node*2 +1 ,ql,qr); } int main () int n,m; while (scanf ("%d%d" ,&n,&m)!=EOF){ for (int i=1 ;i<=n;i++) scanf ("%d" ,&a[i]); build(1 ,n,1 ); char ope[3 ]; int x,y; while (m--){ scanf ("%s%d%d" ,ope,&x,&y); if (ope[0 ]=='Q' ){ ans=-1 ; query(1 ,n,1 ,x,y); printf ("%d\n" ,ans); } else update(1 ,n,1 ,x,y); } } return 0 ; }
HDU1166 敌兵布阵 链接 敌兵布阵
题意 (1)Add i j,第i个营地增加j个人(j不超过30)
分析 单点更新,区间求和
参考代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 #include <stdio.h> const int N=50000 ;int a[N+10 ],tree[N*2 +10 ],ans;using namespace std ;void pushUp (int node) tree[node]=tree[node*2 ]+tree[node*2 +1 ]; } void build (int l,int r,int node) if (l==r){ tree[node]=a[l]; return ; } int mid=(l+r)>>1 ; build(l,mid,node*2 ); build(mid+1 ,r,node*2 +1 ); pushUp(node); } void update (int l,int r,int node,int pos,int val) if (l==r){ tree[node]+=val; return ; } int mid=(l+r)>>1 ; if (mid>=pos) update(l,mid,node*2 ,pos,val); else update(mid+1 ,r,node*2 +1 ,pos,val); pushUp(node); } void query (int l,int r,int node,int ql,int qr) if (ql<=l&&r<=qr){ ans+=tree[node]; return ; } int mid=(l+r)>>1 ; if (mid>=ql) query(l,mid,node*2 ,ql,qr); if (mid<qr) query(mid+1 ,r,node*2 +1 ,ql,qr); } int main () int n,T; scanf ("%d" ,&T); for (int k=1 ;k<=T;k++){ printf ("Case %d:\n" ,k); scanf ("%d" ,&n); for (int i=1 ;i<=n;i++) scanf ("%d" ,&a[i]); build(1 ,n,1 ); char ope[10 ]; int x,y; while (scanf ("%s" ,ope)!=EOF){ if (ope[0 ]=='E' ) break ; scanf ("%d%d" ,&x,&y); if (ope[0 ]=='Q' ){ ans=0 ; query(1 ,n,1 ,x,y); printf ("%d\n" ,ans); } else if (ope[0 ]=='A' ) update(1 ,n,1 ,x,y); else update(1 ,n,1 ,x,-y); } } return 0 ; }
Hdu 1394 Minimum Inversion Number 链接 Minimum Inversion Number
题意 给一个长度为n的序列(n<=5000),由0~n-1的数字组成。
分析 一个数的逆序数为 位置在它前面且比它大的数的个数一个序列的逆序数为每个数的逆序数之和
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 #include <stdio.h> #include <string.h> #define min(a,b) a<b?a:b const int N=5050 ;int tree[N<<1 ],a[N];int query (int l,int r,int node,int ql,int qr) int cnt=0 ; if (ql<=l&&r<=qr) return tree[node]; int mid=(l+r)>>1 ; if (ql<=mid) cnt+=query(l,mid,node<<1 ,ql,qr); if (mid<qr) cnt+=query(mid+1 ,r,node<<1 |1 ,ql,qr); return cnt; } void pushUp (int node) tree[node]=tree[node<<1 ]+tree[node<<1 |1 ]; } void update (int l,int r,int node,int x) if (l==r){ tree[node]++; return ; } int mid=(l+r)>>1 ; if (x<=mid) update(l,mid,node<<1 ,x); else update(mid+1 ,r,node<<1 |1 ,x); pushUp(node); } int main () int n; while (scanf ("%d" ,&n)!=EOF){ int sum=0 ; memset (tree,0 ,sizeof (tree)); for (int i=0 ;i<n;i++){ scanf ("%d" ,&a[i]); sum+=query(0 ,n-1 ,1 ,a[i],n-1 ); update(0 ,n-1 ,1 ,a[i]); } int ans=sum; for (int i=0 ;i<n;i++){ sum-=a[i]; sum+=n-1 -a[i]; ans=min(ans,sum); } printf ("%d\n" ,ans); } return 0 ; }
POJ 2182 & Hdu 2771 Lost Cows 链接 POJ 2182 Hdu 2771
题意 有n头牛,编号为1—n,已知n-1个数,表示站在第i个位置的牛
分析 没想到这题能用线段树做,线段树的运用真广泛啊1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 #include <stdio.h> const int N=9000 ;int tree[N<<1 ],a[N],ans[N];void build (int l,int r,int node) tree[node]=r-l+1 ; if (l==r) return ; int mid=(l+r)>>1 ; build(l,mid,node<<1 ); build(mid+1 ,r,node<<1 |1 ); } int update (int l,int r,int node,int pos) tree[node]--; if (l==r) return l; int mid=(l+r)>>1 ; if (pos<=tree[node<<1 ]) return update(l,mid,node<<1 ,pos); else { pos-=tree[node<<1 ]; return update(mid+1 ,r,node<<1 |1 ,pos); } } int main () int n; while (scanf ("%d" ,&n)!=EOF){ for (int i=2 ;i<=n;i++) scanf ("%d" ,&a[i]); a[1 ]=0 ; build(1 ,n,1 ); for (int i=n;i>=1 ;i--) ans[i]=update(1 ,n,1 ,a[i]+1 ); for (int i=1 ;i<=n;i++) printf ("%d\n" ,ans[i]); } return 0 ; }
Hdu 2795 Billboard 链接 Billboard
题意 有一块h*w的矩形广告板,给n个1*wi的广告,要把广告贴到广告板上,
分析 要知道广告贴在哪,则必须知道每个高度最多还能贴宽度为多少的广告1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 #include <stdio.h> #include <algorithm> const int N=200010 ;using namespace std ;int h,w,n,tree[N<<2 ];void pushUp (int node) tree[node]=max(tree[node<<1 ],tree[node<<1 |1 ]); } void build (int l,int r,int node) tree[node]=w; if (l==r) return ; int mid=(l+r)>>1 ; build(l,mid,node<<1 ); build(mid+1 ,r,node<<1 |1 ); } int query (int l,int r,int node,int val) if (l==r){ tree[node]-=val; return l; } int mid=(l+r)>>1 ; int ans=-1 ; if (tree[node<<1 ]>=val) ans=query(l,mid,node<<1 ,val); else ans=query(mid+1 ,r,node<<1 |1 ,val); pushUp(node); return ans; } int main () while (scanf ("%d%d%d" ,&h,&w,&n)!=EOF){ h=min(h,n); build(1 ,h,1 ); for (int i=1 ;i<=n;i++){ int aw; scanf ("%d" ,&aw); if (tree[1 ]<aw) printf ("-1\n" ); else printf ("%d\n" ,query(1 ,h,1 ,aw)); } } return 0 ; }
POJ 2828 Buy Tickets 链接 Buy Tickets
题意 有N个人去买票,第i个人有一个值$val_i$,他会插到第$pos_i$人的后面,求最后队的顺序
分析 插队问题,单点更新
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 #include <stdio.h> #include <string.h> #include <algorithm> using namespace std ;const int N = 200010 ;int tree[N << 2 ], pos[N], val[N], ans[N];void pushUp (int node) tree[node] = tree[node << 1 ] + tree[node << 1 | 1 ]; } void build (int l, int r, int node) if (l == r) { tree[node] = 1 ; return ; } int mid = (l + r) >> 1 ; build(l, mid, node << 1 ); build(mid + 1 , r, node << 1 | 1 ); pushUp(node); } void update (int l, int r, int node, int pos, int val) if (l == r) { ans[l] = val; tree[node]--; return ; } int mid = (l + r) >> 1 ; if (tree[node << 1 ] >= pos) update(l, mid, node << 1 , pos, val); else { pos -= tree[node << 1 ]; update(mid + 1 , r, node << 1 | 1 , pos, val); } pushUp(node); } int main () int n; while (scanf ("%d" , &n) != EOF) { for (int i = 1 ; i <= n; i++) scanf ("%d%d" , &pos[i], &val[i]); build(1 , n, 1 ); for (int i = n; i >= 1 ; i--) update(1 , n, 1 , pos[i] + 1 , val[i]); for (int i = 1 ; i < n; i++) printf ("%d " , ans[i]); printf ("%d\n" , ans[n]); } return 0 ; }
区间更新 HDU 1698 Just a Hook 链接 Just a Hook
题意 一个hook由n个连续的相同长度的金属棍组成,hook中的金属初始都为铜
分析 解法1:线段树更新区间,求区间和
参考代码 (线段树) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 #include <stdio.h> #include <iostream> const int N=100000 ;using namespace std ;struct stu{ int sum,mark; }tree[N*4 +10 ]; void pushUp (int node) tree[node].sum=tree[node*2 ].sum+tree[node*2 +1 ].sum; } void build (int l,int r,int node) tree[node].mark=-1 ; if (l==r){ tree[node].sum=1 ; return ; } int mid=(l+r)>>1 ; build(l,mid,node*2 ); build(mid+1 ,r,node*2 +1 ); pushUp(node); } void pushDown (int l,int r,int node) if (tree[node].mark!=-1 ){ tree[node*2 ].mark=tree[node*2 +1 ].mark=tree[node].mark; int mid=(l+r)>>1 ; tree[node*2 ].sum=(mid-l+1 )*tree[node].mark; tree[node*2 +1 ].sum=(r-mid)*tree[node].mark; tree[node].mark=-1 ; } } void update (int l,int r,int node,int x,int y,int z) if (x<=l&&r<=y){ tree[node].sum=z*(r-l+1 ); tree[node].mark=z; return ; } pushDown(l,r,node); int mid=(l+r)>>1 ; if (mid>=x) update(l,mid,node*2 ,x,y,z); if (mid<y) update(mid+1 ,r,node*2 +1 ,x,y,z); pushUp(node); } int main () int n,q,T; scanf ("%d" ,&T); for (int k=1 ;k<=T;k++){ scanf ("%d%d" ,&n,&q); build(1 ,n,1 ); while (q--){ int x,y,z; scanf ("%d%d%d" ,&x,&y,&z); update(1 ,n,1 ,x,y,z); } printf ("Case %d: The total value of the hook is %d.\n" ,k,tree[1 ].sum); } return 0 ; }
暴力求解 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 #include <stdio.h> const int N=100000 ;struct stu{ int l,r,val; }a[N]; int main () int n,q,T; scanf ("%d" ,&T); for (int k=1 ;k<=T;k++){ scanf ("%d%d" ,&n,&q); for (int i=1 ;i<=q;i++) scanf ("%d%d%d" ,&a[i].l,&a[i].r,&a[i].val); int sum=n; for (int i=1 ;i<=n;i++) for (int j=q;j>=1 ;j--) if (a[j].l<=i&&i<=a[j].r){ sum+=a[j].val-1 ; break ; } printf ("Case %d: The total value of the hook is %d.\n" ,k,sum); } return 0 ; }
POJ 3468 A Simple Problem with Integers 链接 A Simple Problem with Integers
题意 ‘C’ a b c: 将[a,b]区间的每一个值增加 c
分析 线段树区间更新,区间求和,用延迟标记法优化时间
参考代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 #include <stdio.h> #define LL __int64 const int N=100000 ;struct stu{ LL sum,mark; }tree[N<<2 ]; LL a[N+10 ],sum; void pushUp (int node) tree[node].sum=tree[node<<1 ].sum+tree[node<<1 |1 ].sum; } void pushDown (int l,int r,int node) if (tree[node].mark){ tree[node<<1 ].mark+=tree[node].mark; tree[node<<1 |1 ].mark+=tree[node].mark; int mid=(l+r)>>1 ; tree[node<<1 ].sum+=(mid-l+1 )*tree[node].mark; tree[node<<1 |1 ].sum+=(r-mid)*tree[node].mark; tree[node].mark=0 ; } } void build (int l,int r,int node) tree[node].mark=0 ; if (l==r){ tree[node].sum=a[l]; return ; } int mid=(l+r)>>1 ; build(l,mid,node<<1 ); build(mid+1 ,r,node<<1 |1 ); pushUp(node); } void update (int l,int r,int node,int a,int b,LL c) if (a<=l&&r<=b){ tree[node].mark+=c; tree[node].sum+=c*(r-l+1 ); return ; } pushDown(l,r,node); int mid=(l+r)>>1 ; if (a<=mid) update(l,mid,node<<1 ,a,b,c); if (mid<b) update(mid+1 ,r,node<<1 |1 ,a,b,c); pushUp(node); } void query (int l,int r,int node,int a,int b) if (a<=l&&r<=b){ sum+=tree[node].sum; return ; } pushDown(l,r,node); int mid=(l+r)>>1 ; if (a<=mid) query(l,mid,node<<1 ,a,b); if (mid<b) query(mid+1 ,r,node<<1 |1 ,a,b); } int main () int n,m; scanf ("%d%d" ,&n,&m); for (int i=1 ;i<=n;i++) scanf ("%I64d" ,&a[i]); build(1 ,n,1 ); while (m--){ char ope[3 ]; int a,b; scanf ("%s" ,ope); if (ope[0 ]=='Q' ){ scanf ("%d%d" ,&a,&b); sum=0 ; query(1 ,n,1 ,a,b); printf ("%I64d\n" ,sum); } else { LL c; scanf ("%d%d%I64d" ,&a,&b,&c); update(1 ,n,1 ,a,b,c); } } return 0 ; }
POJ 2528 Mayor’s posters 链接 Mayor’s posters
题意 有n张不同的海报,海报的高相等,依次给出海报所贴的左右区间[l,r]
分析 若有5张海报
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 #include <stdio.h> #include <string.h> #include <algorithm> using namespace std ;const int N = 10010 ;int id[N <<2 ], tree[N << 4 ];bool vis[N];struct stu { int l, r; } ope[N]; void pushdown (int node) if (tree[node]) { tree[node << 1 ] = tree[node << 1 | 1 ] = tree[node]; tree[node] = 0 ; } } void update (int l, int r, int node, int ul, int ur, int color) if (ul <= l && r <= ur) { tree[node] = color; return ; } pushdown(node); int mid = (l + r) >> 1 ; if (ul <= mid) update(l, mid, node << 1 , ul, ur, color); if (mid < ur) update(mid + 1 , r, node << 1 | 1 , ul, ur, color); } int query (int l, int r, int node) if (tree[node]){ if (!vis[tree[node]]){ vis[tree[node]]=true ; return 1 ; } return 0 ; } if (l==r) return 0 ; int ans = 0 ; int mid = (l + r) >> 1 ; ans += query(l, mid, node << 1 ); ans += query(mid + 1 , r, node << 1 | 1 ); return ans; } int main () int n, T; scanf ("%d" , &T); while (T--) { scanf ("%d" , &n); int m = 1 ; for (int i = 1 ; i <= n; i++) { scanf ("%d%d" , &ope[i].l, &ope[i].r); id[m++] = ope[i].l; id[m++] = ope[i].r; } sort(id + 1 , id + m); m = unique(id + 1 , id + m) - id; for (int i = m - 1 ; i > 1 ; i--) if (id[i] - id[i - 1 ] > 1 ) id[m++] = id[i - 1 ] + 1 ; sort(id + 1 , id + m); memset (tree, 0 , sizeof (tree)); for (int i = 1 ; i <= n; i++) { int l = lower_bound(id + 1 , id + m, ope[i].l)-id; int r = lower_bound(id + 1 , id + m, ope[i].r)-id; update(1 , m - 1 , 1 , l, r, i); } memset (vis, false , sizeof (vis)); int ans = query(1 , m - 1 , 1 ); printf ("%d\n" , ans); } return 0 ; }
POJ 2777 Count Color 链接 Count Color
题意 有一个长为L的板,初始颜色为颜色1,有T种颜色,现要进行O次操作
分析 区间更新,延迟标记
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 #include <stdio.h> #include <string.h> #include <algorithm> using namespace std ;const int N = 100010 ;struct stu { int color; bool flag; } tree[N << 2 ]; void build (int l, int r, int node) tree[node].flag = false ; tree[node].color = 1 ; if (l == r) return ; int mid = (l + r) >> 1 ; build(l, mid, node << 1 ); build(mid + 1 , r, node << 1 | 1 ); } void pushDown (int node) if (tree[node].flag) { tree[node].flag = false ; tree[node << 1 ].flag = tree[node << 1 | 1 ].flag = true ; tree[node << 1 ].color = tree[node << 1 | 1 ].color = tree[node].color; } } void pushUp (int node) tree[node].color = tree[node << 1 ].color | tree[node << 1 | 1 ].color; } void update (int l, int r, int node, int ul, int ur, int color) if (ul <= l && r <= ur) { tree[node].color = color; tree[node].flag = true ; return ; } pushDown(node); int mid = (l + r) >> 1 ; if (ul <= mid) update(l, mid, node << 1 , ul, ur, color); if (mid < ur) update(mid + 1 , r, node << 1 | 1 , ul, ur, color); pushUp(node); } int query (int l, int r, int node, int ql, int qr) if (ql <= l && r <= qr) return tree[node].color; pushDown(node); int mid = (l + r) >> 1 , ans = 0 ; if (ql <= mid) ans |= query(l, mid, node << 1 , ql, qr); if (mid < qr) ans |= query(mid + 1 , r, node << 1 | 1 , ql, qr); return ans; } int calBit (int n) int cnt = 0 ; while (n) { if (n & 1 ) cnt++; n >>= 1 ; } return cnt; } int main () int n, T, m; scanf ("%d%d%d" , &n, &T, &m); build(1 , n, 1 ); while (m--) { char ope[2 ]; int a, b, c; scanf ("%s%d%d" , ope, &a, &b); if (a > b) swap(a, b); if (ope[0 ] == 'C' ) { scanf ("%d" , &c); update(1 , n, 1 , a, b, 1 <<(c-1 )); } else { int ans = query(1 , n, 1 , a, b); ans = calBit(ans); printf ("%d\n" , ans); } } return 0 ; }
POJ 2886 Who Gets the Most Candies? 链接 Who Gets the Most Candies?
题意 有N个孩子顺时针围成一个圈玩游戏,每个孩子手上有一张带有一个非零整数的卡片,首先第k个孩子出列,若这个孩子手上的卡片值为A(A>0),则下一个出列的是以他为起点顺时针第A个孩子,若为(-A),则为逆时针的第A个孩子。第i个出列的孩子会得到i的因子个数个糖果,已知每个孩子的名字和手上卡片的值,求得到最多的糖果的孩子的名字和最多糖果数目
分析 网上好多题解都是用反素数来做,反素数可以求出第几个出列的孩子得到的糖果数最多
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 #include <stdio.h> #include <string.h> #include <algorithm> using namespace std ;const int N = 500010 ;const int INF = 1000000 ;int cur_i,next_i,ans, ansPos,tree[N << 2 ], p[N];struct stu { char name[15 ]; int val; } child[N]; void calFactor () for (int i=1 ;i<=N-10 ;i++) for (int j=1 ;i*j<=N-10 ;j++) p[i*j]++; } void pushUp (int node) tree[node] = tree[node << 1 ] + tree[node << 1 | 1 ]; } void build (int l, int r, int node) if (l == r) { tree[node] = 1 ; return ; } int mid = (l + r) >> 1 ; build(l, mid, node << 1 ); build(mid + 1 , r, node << 1 | 1 ); pushUp(node); } void update (int l, int r, int node, int pos,int i) if (l == r) { if (p[i] > ans) { ans = p[i]; ansPos = l; } next_i=child[l].val; tree[node]--; return ; } int mid = (l + r) >> 1 ; if (tree[node << 1 ] >= pos) update(l, mid, node << 1 , pos,i); else update(mid + 1 , r, node << 1 | 1 , pos - tree[node << 1 ],i); pushUp(node); } int main () calFactor(); int n, k; while (scanf ("%d%d" , &n, &k) != EOF) { build(1 , n, 1 ); for (int i = 1 ; i <= n; i++) scanf ("%s%d" , child[i].name, &child[i].val); ans = ansPos=-1 ; int pos,ret=n; cur_i=n,next_i=k; for (int i = 1 ; i <= n; i++) { if (next_i>=0 ) cur_i--; pos=(cur_i+next_i%ret+ret)%ret; update(1 , n, 1 , pos+1 ,i); cur_i=pos; ret--; } printf ("%s %d\n" , child[ansPos].name, ans); } return 0 ; }