树状数组 | happy

树状数组(BIT)是与线段树类似的数据结构，用来处理区间修改查询问题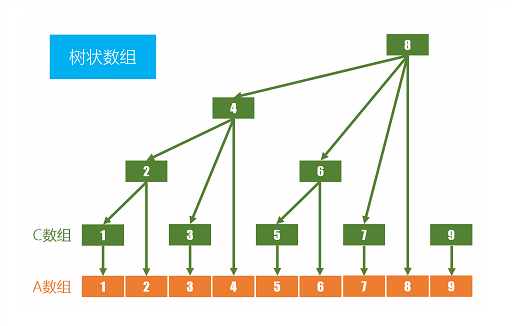
BIT

一维树状数组

如上图所示，若用树状数组求a数组的和
c[1]=a[1];
c[2]=a[1]+a[2];
c[3]=a[3];
c[4]=a[1]+a[2]+a[3]+a[4];
c[5]=a[5];
c[6]=a[5]+a[6];
c[7]=a[7];
c[8]= a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8];
将十进制化成二进制，然后观察这些二进制数最右边1的位置：
1 —> 00000001 —>1
2 —> 00000010 —>2
3 —> 00000011 —>1
4 —> 00000100 —>4
5 —> 00000101 —>1
6 —> 00000110 —>2
7 —> 00000111 —>1
8 —> 00001000 —>8
由此我们可以得出结论：c[i]=a[i]+a[i-1]+…+a[i-k+1]
其中k为i的二进制数中从右往左第一个1的权值即k=lowbit(i)=i&(-i)
证明：设A’为A的二进制反码，i的二进制表示成A1B，其中A不管，B为全0序列。
那么-i=A’0B’+1。由于B为全0序列，那么B’就是全1序列，所以-i=A’1B，所以：
i&(-i)= A1B& A’1B=1B，即k=i&(-i)

void update(int pos,int x)  //将a[pos]增加x
{
    for(int i=pos;i<=n;i+=lowbit(i))
        c[i]+=x;
}
int query(int x)  //查询[1,n]的和
{
    int ans=0;
    for(int i=x;i>=1;i-=lowbit(i))
        ans+=c[i];
    return ans;
}

若查询[l,r]的和，可以先查询sum[1,r],sum[1,l-1],sum[l,r]=sum[1,r]-sum[1,l-1]

二维树状数组

推广到二维数组
c[1][1]=a[1][1];
c[1][2]=a[1][1]+a[1][2];
c[1][3]=a[1][3];
c[1][4]=a[1][1]+a[1][2]+a[1][3]+a[1][4];
c[1][5]=a[1][5];
c[1][6]=a[1][5]+a[1][6];
c[1][7]=a[1][7];
…
c[1][1]=a[1][1];
c[2][1]=a[1][1]+a[2][1];
c[3][1]=a[3][1];
c[4][1]=a[1][1]+a[2][1]+a[3][1]+a[4][1];
c[5][1]=a[5][1];
c[6][1]=a[5][1]+a[6][1];
c[7][1]=a[7][1];
…
c[2][6]=a[1][5]+a[1][6]+a[2][5]+a[2][6];
可得对于c[i][j],k1=lowbit(i)=i&(-i),i可取{i,i-1,…,i-k1+1},
k2=lowbit(j)=j&(-j),j可取{j,j-1,…,j-k2+1}
c[i][j]=∑c[i,{j,j-1,…j-k2+1}]+∑c[i-1,{j,j-1,…j-k2+1}]+∑c[i-k1+1,{j,j-1,…j-k2+1}]
对于W*H的二维BIT只需建立H个大小为x轴方向元素个数W个BIT，然后把这些BIT通过y轴方向管理起来就可以了。也就是说，y方向的BIT的每个元素不是整数，而是一个x轴方向的BIT。
这样所有操作的复杂度为O(logW*logH).用同样的方法可以扩展到更高维度的情况。

void update(int x, int y, int val) //将a[x][y]的值增加val
{
    for (int i = x; i <=n; i += lowbit(i))
        for (int j = y; j <=n; j += lowbit(j)) 
            c[i][j] += val;
}
int query(int x, int y)    //查询 1<=i<=x,1<=j<=y的和
{
    int ans = 0;
    for (int i = x; i >= 1; i -= lowbit(i))
        for (int j = y; j >= 1; j -= lowbit(j))
            ans += c[i][j];
    return ans;
}

若需要求l1<=x<=r1,l2<=y<=r2的和
s1=sum[1<=i<=r1 ,1<=j<=r2]
s2=sum[1<=i<=l1-1,1<=j<=r2]
s3=sum[1<=i<=r1 ,1<=j<=l2-1]
s4=sum[1<=i<=l1-1,1<=j<=l2-1]
根据容斥定理得 sum[l1<=x<=r1,l2<=y<=r2]=s1-s2-s3+s4